News

Graphically analysing and statistically testing influence factors in a process

18
Dec

Stel je voor dat je een proces in kaart hebt gebracht en je hebt al mogelijke invloedfactoren geïdentificeerd. De volgende stap is om te bepalen of deze factoren echt invloed hebben op het proces en hoeveel invloed ze hebben. Maar hoe pak je dat aan?

Trechter van analyse van invloedfactoren

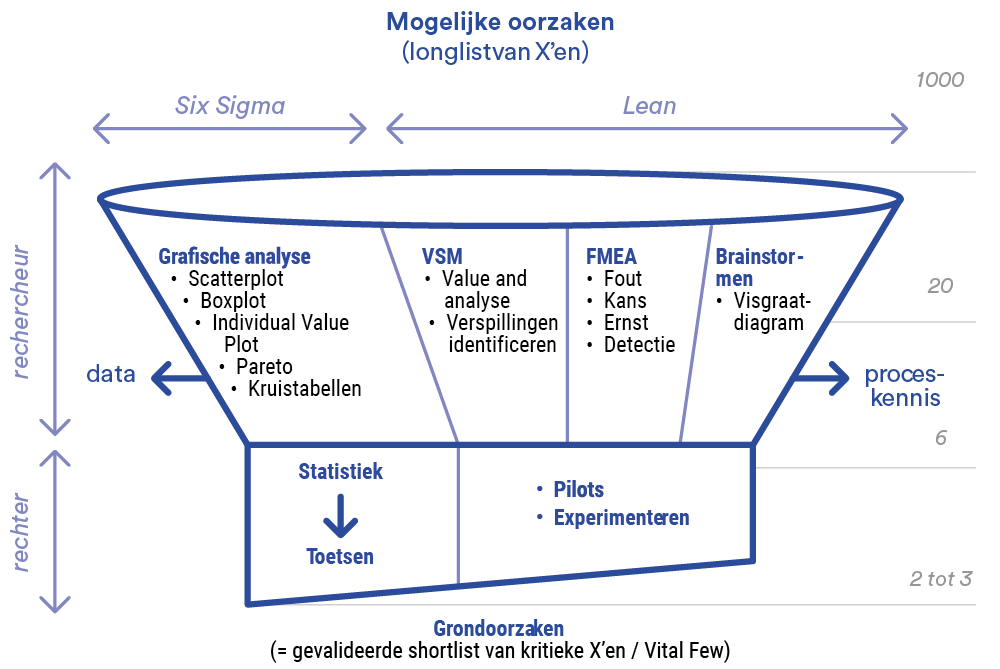
Het analyseren van invloedfactoren kun je vergelijken met een trechter: je begint met een breed scala aan mogelijkheden en filtert die stapsgewijs tot een kleinere groep van echte oorzaken. Eerst sluit je factoren uit die duidelijk geen invloed hebben, daarna onderzoek je de resterende factoren grondiger. Dit proces lijkt op het werk van een detective die aanwijzingen verzamelt en een rechter die op basis van feiten een oordeel velt (figuur 1).

Figuur 1: Trechter van analyse van invloedfactoren

Proceskennis en data-analyse

Bij het identificeren van invloedfactoren gebruik je enerzijds proceskennis en anderzijds data-analyse. Als je data beschikbaar hebt, begin je vaak met een visuele analyse om patronen te herkennen. Daarna gebruik je statistische toetsen om te bepalen of de verbanden die je vermoedt ook daadwerkelijk bestaan. In dit artikel bespreek ik deze twee stappen: grafische analyse and statistische toetsen.

Stap 1: Grafische analyse – patronen ontdekken

Om te starten bepaal je welke meetbare aspecten van het proces invloed hebben op de prestaties. Deze worden de Critical to Quality-aspecten (CTQ’s) genoemd.

Denk bijvoorbeeld aan doorlooptijd, een veelgebruikte procesprestatie-indicator. Vervolgens identificeer je mogelijke invloedfactoren, zoals de ervaring van medewerkers.

De data die je verzamelt, kan continu zijn (bijvoorbeeld doorlooptijd in minuten) of categorisch (bijvoorbeeld ervaringsniveau: junior, medior of senior). Afhankelijk van het datatype kies je een passende grafische analysemethode, zoals in dit voorbeeld een boxplot (zie tabel 1).

Voorbeeld grafische analyse

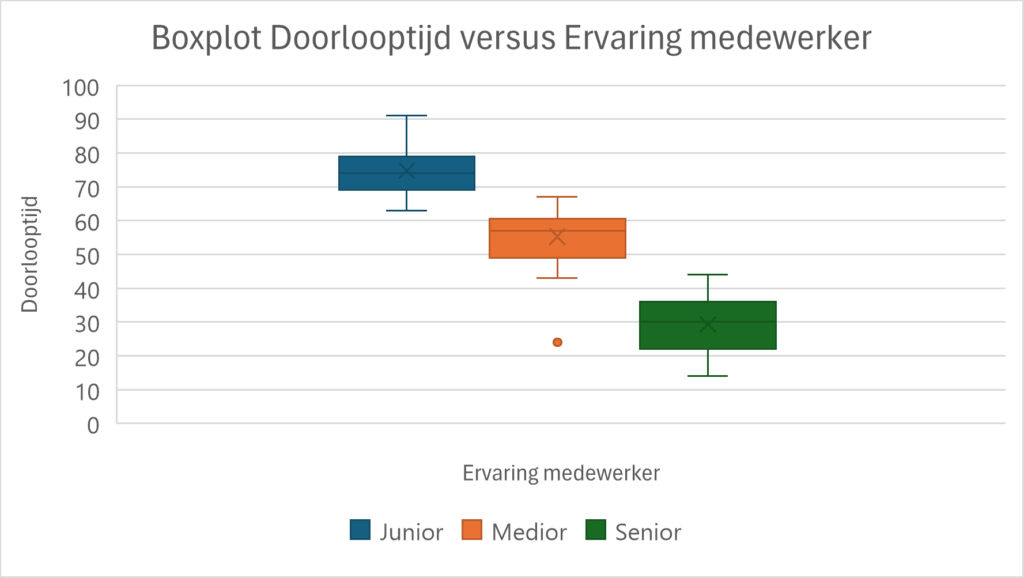
Stel dat je wilt onderzoeken of de ervaring van medewerkers de doorlooptijd beïnvloedt. Met een boxplot, die groepsverschillen visueel weergeeft, kun je snel mogelijke verschillen tussen groepen ontdekken. In figuur 2 wordt duidelijk dat junior medewerkers doorgaans langere doorlooptijden hebben dan medioren en senioren, wat suggereert dat ervaring een rol speelt.

Stap 2: Statistische toets – verbanden bevestigen

Na de grafische analyse heb je misschien al een idee of er een verband is tussen de ervaring van medewerkers en de doorlooptijd. Maar om er zeker van te zijn, wil je dit testen met een statistische toets. Wanneer je met grafieken patronen hebt geïdentificeerd, kun je statistische toetsen inzetten om te beoordelen of deze verbanden daadwerkelijk significant zijn.

In het voorbeeld gebruik je een ANOVA-toets, die groepsgemiddelden vergelijkt, omdat je de doorlooptijd (continue data) wilt analyseren in relatie tot verschillende ervaringsniveaus (categorische data) (zie tabel 2).

De analyse bestaat uit twee stappen:

  1. Controleren van aannames: Voordat je de resultaten van de ANOVA kunt interpreteren, controleer je of de data voldoet aan de aannames van de toets. Dit omvat bijvoorbeeld een residuenanalyse om te beoordelen of de data normaal verdeeld is en of de varianties tussen groepen gelijk zijn.
  2. Resultaten interpreteren: Als de aannames valide zijn, analyseer je de groepsgemiddelden. Hiermee bepaal je of er een significant verschil is tussen de ervaringsniveaus met betrekking tot de doorlooptijd.

Door deze stappen te volgen, kun je met meer zekerheid uitspraken doen over het verband tussen ervaring en doorlooptijd.

Let op: aannames controleren bij statistische toetsen

Voordat je een statistische toets zoals ANOVA toepast, is het belangrijk om te controleren of de data voldoet aan de benodigde aannames. Voor de ANOVA betekent dit onder andere dat de residuen normaal verdeeld moeten zijn en dat de varianties tussen de groepen gelijk zijn. Wanneer de data niet aan deze aannames voldoet, kun je overwegen om een alternatieve toets te gebruiken, zoals de Kruskal-Wallis-toets. Deze niet-parametrische toets heeft minder strenge aannames en is geschikt voor data die niet normaal verdeeld is.

Stap 2a: Controleer aannames – residuenanalyse

Voordat je de ANOVA-resultaten kunt vertrouwen, controleer je of de data voldoet aan de aannames, zoals normaliteit. Dit doe je met een residuenanalyse. Residuen zijn de verschillen tussen de geobserveerde waarden en de voorspelde waarden van het model. Door deze residuen te analyseren, controleer je of ze willekeurig verdeeld zijn en voldoen aan de normaliteitsaannames.

Bij zo’n statistische toets formuleer je twee hypotheses:

  • De nulhypothese: De residuen zijn normaal verdeeld.
  • De alternatieve hypothese: De residuen zijn niet normaal verdeeld.

De p-waarde uit de toets geeft de kans dat je een afwijking van normaliteit zou observeren, als de nulhypothese waar is. Een p-waarde groter dan 0,05 betekent dat er onvoldoende bewijs is om de nulhypothese te verwerpen. Anders gezegd, er is geen sterke aanwijzing dat de residuen niet normaal verdeeld zijn. Daarom accepteren we de nulhypothese in dit geval: de residuen zijn normaal verdeeld.

In ons voorbeeld is de p-waarde 0,343, wat groter is dan 0,05. Dit betekent dat de kans op een dergelijke afwijking onder de nulhypothese groot genoeg is en dat de residuen voldoen aan de normaliteitsaannames. Hierdoor kunnen we de ANOVA veilig toepassen en de resultaten als betrouwbaar beschouwen. Als de normaliteit niet wordt bevestigd, kun je, zoals eerder aangegeven, alternatieve niet-parametrische toetsen, zoals de Kruskal-Wallis-toets, overwegen.

Stap 2b: Resultaten interpreteren – analyse van gemiddelden

De ANOVA-toets toont aan dat er een significant verschil is in doorlooptijden tussen de groepen. Bij deze toets formuleer je twee hypothesen:

  • De nulhypothese: Er is geen verschil in de gemiddelde doorlooptijden tussen de groepen (ervaring speelt geen rol).
  • De alternatieve hypothese: Er is minstens één groep waarvan de gemiddelde doorlooptijd significant verschilt (ervaring speelt een rol).

De p-waarde uit de ANOVA-toets geeft de kans dat je de geobserveerde verschillen of grotere verschillen in groepsgemiddelden ziet, als de nulhypothese waar is. Wanneer de p-waarde kleiner is dan 0,05, betekent dit dat de kans op zulke verschillen bij een juiste nulhypothese zeer klein is. We verwerpen in dat geval de nulhypothese en accepteren de alternatieve hypothese: er is een significant verschil in doorlooptijden tussen de groepen, en ervaring speelt dus een rol.

In ons voorbeeld bevestigt een p-waarde kleiner dan 0,05 dat ervaring daadwerkelijk een effect heeft op de doorlooptijden. De verklaring hiervoor is gebaseerd op proceskennis: junior medewerkers werken vaak onder begeleiding, wat extra tijd kan kosten (figuur 3).

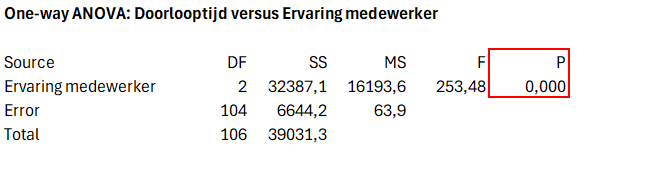
Figuur 3: ANOVA-resultaten

Conclusie: visueel en statistisch onderbouwen

Door grafische analyse te combineren met statistische toetsen, kun je niet alleen verbanden visualiseren, maar ook objectief bepalen of ze echt bestaan. Dit maakt het mogelijk om op feiten gebaseerde verbeteringen door te voeren in je proces.